In today’s fast-paced business world, the ability to predict future trends is not just a valuable skill—it’s a necessity. Whether it’s estimating next quarter’s sales, forecasting demand for a new product, or analyzing seasonal fluctuations in the market, businesses rely heavily on time series analysis. This statistical technique helps organizations identify patterns in historical data and make data-driven decisions for the future.
In this article, we’ll explore the components of time series data, methods for trend measurement, and how these concepts are applied in business forecasting.
Download UNIT 3 – Time Series Analysis and Forecasting Notes
Get simplified revision notes for this unit:
⬇️
Download Unit 3 Notes PDF
What is Time Series Analysis?
A time series is a sequence of observations recorded at regular time intervals—daily, weekly, monthly, or annually. Examples include:
Monthly sales of a retail store
Daily stock prices of a company
Annual rainfall statistics
Time series analysis involves examining this data to detect patterns and trends. Once these patterns are identified, they can be used to forecast future values.
Components of Time Series Data
Time series data typically consists of four main components:
1. Trend (T)
The trend is the long-term movement or direction in the data. It shows the general tendency of the data to increase, decrease, or remain stable over time.
Example: Over the last 10 years, the global smartphone market has shown a consistent upward trend in sales, even though there are seasonal fluctuations.
Business Impact: Identifying the trend helps in long-term planning, such as expansion strategies or investment decisions.
2. Seasonal Variation (S)
Seasonal variation refers to patterns that repeat at regular intervals within a year due to seasonal factors such as weather, festivals, or holidays.
Example: Ice cream sales peak during summer months and drop during winter.
Business Impact: Seasonal adjustments help companies plan inventory, marketing campaigns, and staffing needs.
3. Cyclical Variation (C)
Cyclical variation occurs due to economic cycles like booms and recessions. These changes are usually observed over longer periods and are influenced by broader economic conditions.
Example: Automobile sales often rise during economic growth and decline during recessions.
Business Impact: Recognizing cyclical trends helps in adjusting production and investment decisions according to the economic climate.
4. Irregular or Random Variation (I)
This component represents unpredictable fluctuations caused by events like natural disasters, strikes, or sudden policy changes.
Example: A sudden pandemic causing a drop in tourism.
Business Impact: Although these variations can’t be predicted precisely, risk management strategies can help mitigate losses.
Methods for Measuring Trends
To forecast accurately, it’s essential to separate the trend from the other components of a time series. Two popular methods for trend measurement are:
1. Moving Average Method
The moving average method smooths out short-term fluctuations by averaging data over a specific period.
Example: A 3-month moving average for monthly sales data calculates the average of every three consecutive months, providing a clearer view of the long-term trend.
Advantages: Easy to use and reduces the impact of irregular variations.
Limitations: Doesn’t work well when the data has strong seasonal patterns unless adjustments are made.
2. Least Squares Method
This method fits a straight line (or curve) to the data using a mathematical equation:
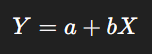
Where:
Y = Dependent variable (e.g., sales)
X = Time
a = Intercept
b = Slope of the trend line
Example:
If a business notices that sales increase by ₹5,000 every quarter, the least squares method can be used to predict future sales by extending the trend line.
Advantages:
Provides a precise mathematical equation for forecasting
Works well for both increasing and decreasing trends
Business Forecasting with Time Series
Forecasting is the process of predicting future values based on historical data. In business, accurate forecasts can:
Guide production planning
Inform budgeting and financial planning
Support marketing strategy development
Steps in Time Series Forecasting
Data Collection – Gather accurate and relevant historical data.
Data Cleaning – Remove errors, fill missing values, and adjust for outliers.
Identifying Components – Separate trend, seasonal, cyclical, and irregular variations.
Model Selection – Choose a forecasting method (e.g., moving average, exponential smoothing, regression analysis).
Forecasting – Use the model to predict future values.
Evaluation – Compare forecasts with actual results to improve accuracy.
Practical Example – Sales Forecasting
Let’s say a clothing retailer wants to forecast monthly sales for the next year.
Step 1: Analyze historical sales data for the past 3 years.
Step 2: Identify seasonal patterns (e.g., high sales during festive months).
Step 3: Calculate the moving average to determine the underlying trend.
Step 4: Adjust forecasts based on seasonal indices.
Step 5: Factor in any expected economic changes (cyclical effects).
By following these steps, the retailer can estimate how much stock to order and when to launch major sales campaigns.
Importance of Time Series Analysis in Business
Better Decision-Making: Data-driven forecasts reduce guesswork.
Cost Control: Helps manage inventory and avoid overproduction.
Market Competitiveness: Anticipating demand allows businesses to respond faster than competitors.
Financial Planning: Predicting cash flows ensures better fund allocation.
Challenges in Time Series Forecasting
Data Quality Issues: Incomplete or inaccurate data can lead to misleading forecasts.
External Shocks: Unforeseen events like natural disasters or political instability can disrupt patterns.
Overfitting Models: Making models too complex can result in poor real-world performance.
