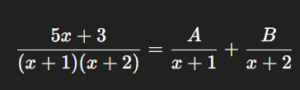Mathematics is often called the “language of science,” and nowhere is this more evident than in the pharmaceutical sciences. Behind every formula, dosage, and chemical process lies a foundation of mathematical concepts. Unit 1 of pharmaceutical mathematics introduces some of these building blocks—partial fractions, logarithms, functions, and limits—that not only sharpen analytical skills but also serve as essential tools in pharmacy and pharmacokinetics.
Download UNIT 1 – Mathematics in Pharmacy: From Fractions to Limits Notes
Get simplified revision notes for this unit:
⬇️
Download Unit 1 Notes PDF
Partial Fractions: Breaking Down the Complex
Introduction to Rational Fractions
At the heart of algebra lies the concept of fractions. When both numerator and denominator are polynomials, we call them rational fractions. These fractions can be proper, when the degree of the numerator is less than that of the denominator, or improper, when the numerator’s degree is equal to or higher.
Resolving into Partial Fractions
A partial fraction is the expression of a complex rational fraction as the sum of simpler fractions. For example:
This process makes complicated algebraic manipulations manageable.
Applications in Pharmacy
Partial fractions are not just abstract algebra—they play a direct role in chemical kinetics and pharmacokinetics. When modeling the rate of drug absorption or elimination, equations often involve rational fractions. By resolving these into partial fractions, scientists can simplify and interpret reaction rates, making it easier to calculate half-lives, drug concentrations, and steady states.
Logarithms: The Power of Exponents Simplified
What Are Logarithms?
A logarithm answers the question: “To what power must a base be raised to obtain a given number?” For example:
log10 1000 = 3since 103 = 1000
Properties of Logarithms
Logarithms obey certain rules that make calculations straightforward:
Product Rule: log(ab)=loga+logb\log(ab) = \log a + \log b
Quotient Rule: log(a/b)=loga−logb\log(a/b) = \log a – \log b
Power Rule: log(an)=nloga\log(a^n) = n \log a
These theorems turn multiplication into addition and exponents into multiplication, reducing complexity.
Characteristic and Mantissa
In common logarithms (base 10), numbers are expressed with a characteristic (the integer part) and a mantissa (the decimal part). For instance:

Here, 3 is the characteristic, and .735 is the mantissa.
Applications in Pharmaceutical Problems
Logarithms are indispensable in pharmacy. They help in pH calculations, determining hydrogen ion concentrations, and analyzing exponential processes such as microbial growth or radioactive decay. Complex pharmacological equations are simplified using log transformations, making them practical for daily calculations in labs and clinics.
Functions: Mapping Inputs to Outputs
Real-Valued Functions
A function is a rule that assigns every input (x) to exactly one output (f(x)). When outputs are real numbers, we call it a real-valued function.
Classification of Functions
Functions come in many forms:
Algebraic functions, such as polynomials and rational functions.
Transcendental functions, including logarithmic, exponential, and trigonometric functions.
In pharmaceutical contexts, functions describe relationships between drug dose and effect, concentration and time, or even enzyme activity and substrate concentration.
Limits and Continuity: The Foundation of Calculus
Understanding Limits
The concept of a limit underpins much of modern mathematics. Informally, the limit of a function describes its behavior as the input approaches a particular value. For example:
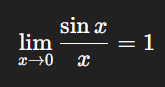
This principle is fundamental in defining derivatives and integrals.
Definition of a Limit
Formally, we say that limx→af(x)=L\lim_{x \to a} f(x) = L if f(x) approaches the value L as x gets closer to a.
Continuity of a Function
A function is continuous if it has no breaks, jumps, or holes at any point in its domain. In other words, you can draw its graph without lifting your pen.
Role in Pharmacy
Limits and continuity are vital in pharmacokinetics for modeling processes such as drug absorption rates, plasma concentration curves, and diffusion phenomena. They help ensure precise calculation of values as conditions change over time.