When pharmacy students first encounter matrices and determinants, the topic may seem more suited for mathematicians than healthcare professionals. Yet, this branch of algebra is a quiet powerhouse in pharmaceutical sciences, particularly in pharmacokinetics, where drug concentrations, reaction pathways, and biological systems are modeled using equations. Unit 2 dives into the fascinating world of matrices, determinants, and their applications—tools that bring order to complex systems.
Download UNIT 2 – Matrices and Determinants: The Algebra Behind Modern Pharmacy Notes
Get simplified revision notes for this unit:
⬇️
Download Unit 2 Notes PDF
Introduction to Matrices
A matrix is simply a rectangular arrangement of numbers, symbols, or expressions in rows and columns. Think of it as a structured way of representing data. For example:
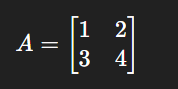
This small square of numbers holds enormous power, allowing us to encode systems of equations and perform algebraic manipulations with precision.
Types of Matrices
Matrices come in different forms:
Row matrix: A matrix with a single row.
Column matrix: A matrix with a single column.
Square matrix: Rows equal columns.
Diagonal and identity matrices: Key players in simplifying calculations.
Zero matrix: Where every entry is zero.
Each type serves unique purposes, from data storage to solving differential equations.
Operations on Matrices
Matrices are not static—they can be manipulated:
Addition and subtraction combine matrices of the same order.
Transpose flips a matrix across its diagonal, turning rows into columns.
Multiplication of matrices is where the real magic happens, particularly in solving simultaneous equations.
In pharmacy, matrix multiplication is used to express drug interactions, where multiple drugs and their effects on biological systems are studied together.
Determinants: Unlocking Matrix Secrets
A determinant is a special number derived from a square matrix. For a 2×2 matrix:
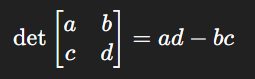
Determinants tell us whether a system of equations has a unique solution and play a role in finding inverses.
Properties of Determinants
Swapping two rows changes the sign.
Multiplying a row by a scalar multiplies the determinant.
If two rows are identical, the determinant becomes zero.
These rules ensure precision in problem-solving.
Minors, Cofactors, and the Adjoint
To dive deeper into determinants, one must learn about minors (determinants of smaller sub-matrices) and cofactors (minors with sign adjustments). Collecting these cofactors forms the adjoint matrix, a vital step in finding the inverse of a matrix.
An inverse matrix exists only when the determinant is non-zero. Non-singular matrices have inverses, while singular matrices do not.
Solving Linear Equations
One of the biggest applications of matrices is solving systems of linear equations. Two important methods dominate:
Matrix method: Expressing equations in the form AX=BAX = B, and solving for X=A−1BX = A^{-1}B.
Cramer’s Rule: A determinant-based method that provides exact solutions for small systems.
For pharmacists, these tools are used in kinetic modeling, where multiple processes—absorption, distribution, and elimination—happen simultaneously.
Advanced Concepts: Characteristic Equation & Cayley–Hamilton Theorem
A square matrix has an associated characteristic equation, derived from det(A−λI)=0\det(A – \lambda I) = 0, where λ\lambda are the roots, also known as eigenvalues. These eigenvalues represent intrinsic properties of the system.
The Cayley–Hamilton theorem is a remarkable result stating that every square matrix satisfies its own characteristic equation. Though theoretical, it has practical significance in solving higher-order equations in system modeling.
Applications in Pharmacokinetics
In pharmacy, matrices move from chalkboards to real-world labs. Pharmacokinetic equations, which track how drugs move through the body, often involve multiple variables and differential equations.
Drug absorption and elimination models can be expressed using systems of equations, solved neatly with matrices.
Compartment models in pharmacokinetics—where the body is treated as one or more “compartments” that exchange drugs—are simplified using determinants and inverses.
Prediction of steady-state concentrations relies on matrix algebra to balance rates of input and output.
For example, in a two-compartment model, drug concentration in plasma and tissues can be expressed in matrix form, making solutions faster and more reliable.
