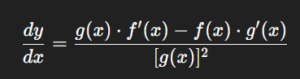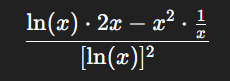In the world of pharmacy and science, change is constant—drugs change concentration in the bloodstream, reactions change speed over time, and populations of molecules change in response to chemical environments. The mathematical tool that captures this idea of change is calculus, and at its heart lies differentiation. Unit 3 introduces students to the foundations of differentiation, its basic rules, and its powerful applications.
Download UNIT 3 – Calculus and Differentiation: The Mathematics of Change Notes
Get simplified revision notes for this unit:
⬇️
Download Unit 3 Notes PDF
What is Differentiation?
Differentiation is the process of finding the derivative of a function. While the definition may sound technical, the idea is simple: it measures the rate of change.
Imagine a drug being absorbed into the body. Its concentration in the blood changes over time. Differentiation allows us to calculate how fast this change happens at any given instant. Just as speed is the rate of change of distance with respect to time, derivatives give us precise ways of tracking change across functions.
Derivative of a Function
The derivative of a function, usually written as f′(x)f'(x) or dydx\frac{dy}{dx}, expresses how the output of the function changes when the input changes slightly.
For instance, if y=x2y = x^2, then the derivative dydx=2x\frac{dy}{dx} = 2x. This tells us that the slope of the curve increases as xx increases, a concept crucial for modeling growth, decay, and rates in pharmacy.
Derivative of a Constant
Some functions do not change at all. Take y=5y = 5, for example. No matter what value xx takes, yy remains fixed. Since differentiation measures change, the derivative of a constant is always zero.
This basic rule serves as the simplest reminder: if there’s no change, the derivative vanishes.
Derivative of a Product of a Constant and a Function
When a constant multiplies a function, the derivative respects the constant but focuses on the function.
Mathematically, if y=k⋅f(x)y = k \cdot f(x), then dydx=k⋅f′(x)\frac{dy}{dx} = k \cdot f'(x).
For example, if y=7x2y = 7x^2, the derivative is 14x14x. The constant 77 remains, while the differentiation applies only to x2x^2.
This rule is widely used in pharmaceutical equations, where rate constants multiply concentration terms.
Derivative of the Sum or Difference of Two Functions
Functions can combine through addition or subtraction. Differentiation handles them separately but smoothly.
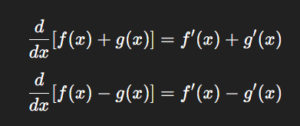
In other words, differentiation distributes across sums and differences.
Imagine two drugs being metabolized at different rates—combining their rate equations is as straightforward as adding or subtracting their derivatives.
Product Formula: Derivative of the Product of Two Functions
One of the most important results in calculus is the product rule.
If y=f(x)⋅g(x)y = f(x) \cdot g(x), then the derivative is:
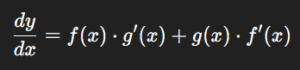
Rather than simply differentiating each function separately, the rule reminds us to consider both the changing function and the product’s structure.
For example, if y=x2⋅sin(x)y = x^2 \cdot \sin(x), the derivative is:
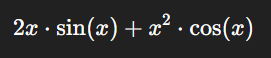
This interplay becomes vital in pharmacy when modeling drug concentration affected simultaneously by two processes, such as absorption and metabolism.
Quotient Formula: Derivative of the Quotient of Two Functions
Equally powerful is the quotient rule, which handles division.
If y=f(x)g(x)y = \frac{f(x)}{g(x)}, then:
The formula may look intimidating, but its logic is simple—it balances how the numerator and denominator change relative to each other.
Take y=x2ln(x)y = \frac{x^2}{\ln(x)}. Using the quotient rule, the derivative becomes:
This is particularly useful in pharmacokinetics, where dose rates are often expressed as ratios of concentration over time.
Why Differentiation Matters in Pharmacy
At first glance, differentiation may seem like abstract mathematics. But in pharmacy, its real-world applications are profound:
Drug absorption and elimination rates are expressed as derivatives of concentration functions.
Reaction rates in chemical kinetics use derivatives to calculate speed at any given moment.
Optimization problems such as finding the maximum effect of a drug dose or minimizing side effects rely on derivatives to determine turning points.
Differentiation, therefore, acts as the language of change in the pharmaceutical sciences.